Information Security

UUG Spring 2023

---

“The three golden rules to ensure computer security are: do not own a computer; do not power it on; and do not use it.” — Robert Morris

---

CIA Triad

• Confidentiality
• Integrity
• Availability

---

Confidentiality

• Assures that private or confidential information is not made available or disclosed to unauthorized individuals

---

Integrity

• Assures that information and programs are changed only in a specified and authorized manner

---

Availability

• Assures that systems work promptly and service is not denied to users

---

Which Aspect of the CIA Triad is Most Important?

---

Additional CIA Triad Concepts

• Authenticity

  • The property of being genuine and being able to be verified and trusted

    • Confidence in the validity of a transmission, a message, or message originator

• Accountability

  • The security goal that generates the requirement for actions of an entity to be traced uniquely to that entity.

    • Non-repudiation

---

Cryptography Concepts

• Plaintext

  • The item we plan on encrypting. Human-readable.

• Key

  • A secret.

• Ciphertext

  • The output of encryption. Not human-readable.

• Cleartext

  • The output of decryption (same as the input plaintext).

---

Kerckhoffs’s principle

• Security must reside entirely in the secret key

• Assume all other information is known by the attacker

• This includes the:

  • key-space (128-bit, 256-bit)
  • algorithm (AES, RSA, ECC)
  • hardware (Enigma)

---

Types of Ciphers

• Block

  • Message is partitioned into fixed-size blocks (typically 64 or 128-bits)

    • DES, AES, RSA

• Stream

  • Encrypts a digital data stream one bit or one byte at a time.

    • RC4, OTP (One-time pad)

---

Electronic Codebook (ECB)

---

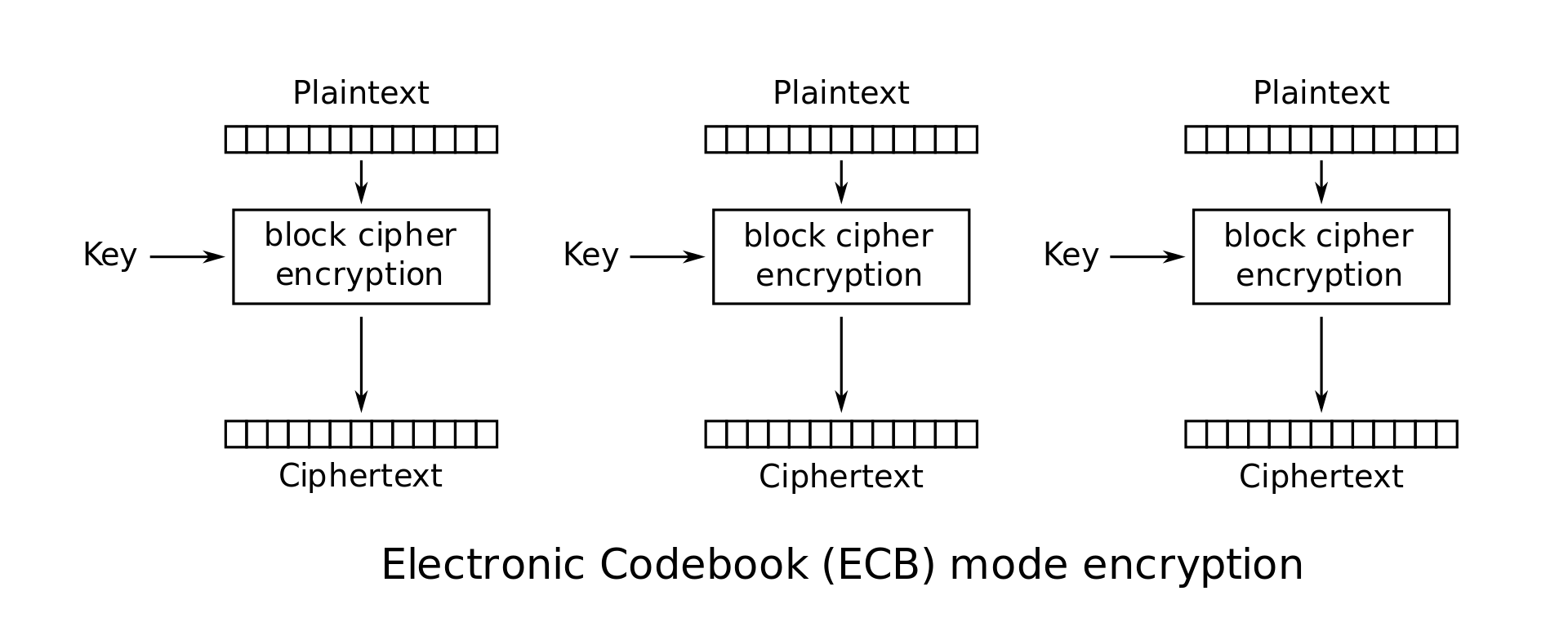
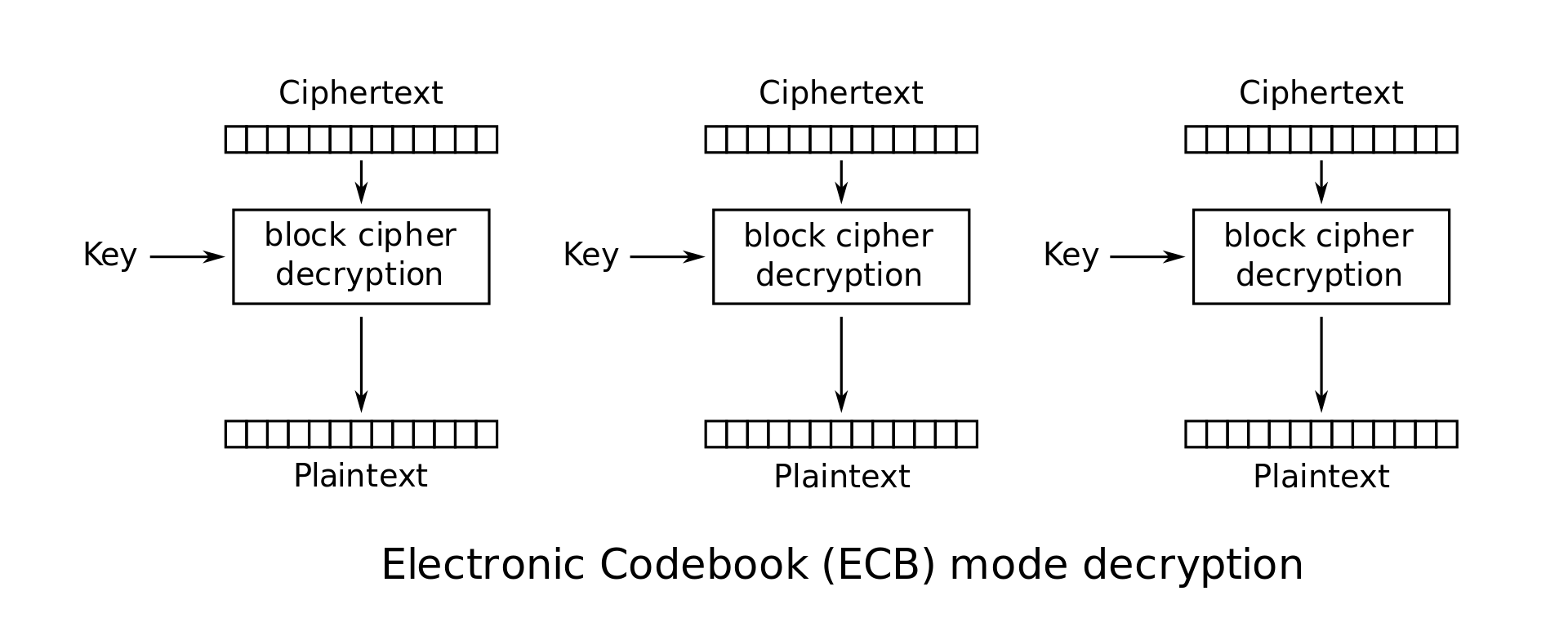
Cipher Block Chaining (CBC)

• Duplicate data is not reflected in ciphertext

• Malformed/incorrect blocks affect all following blocks

---

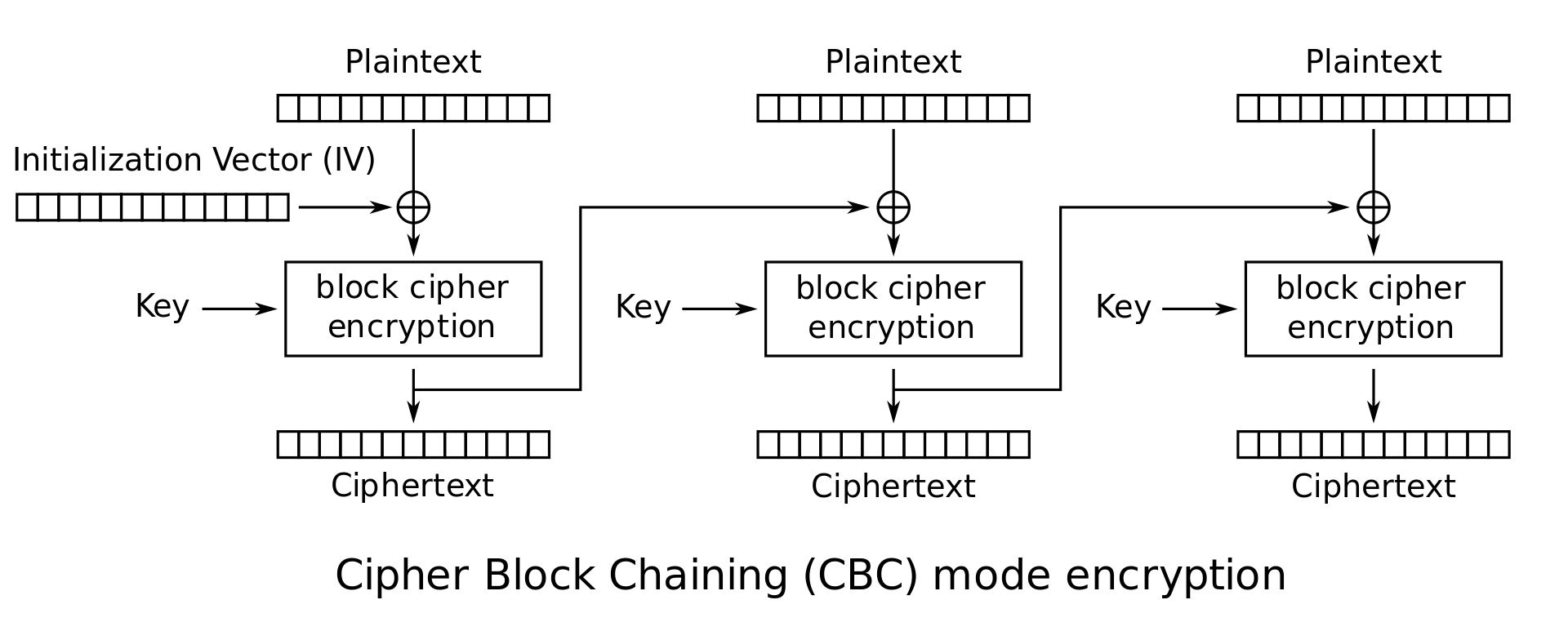
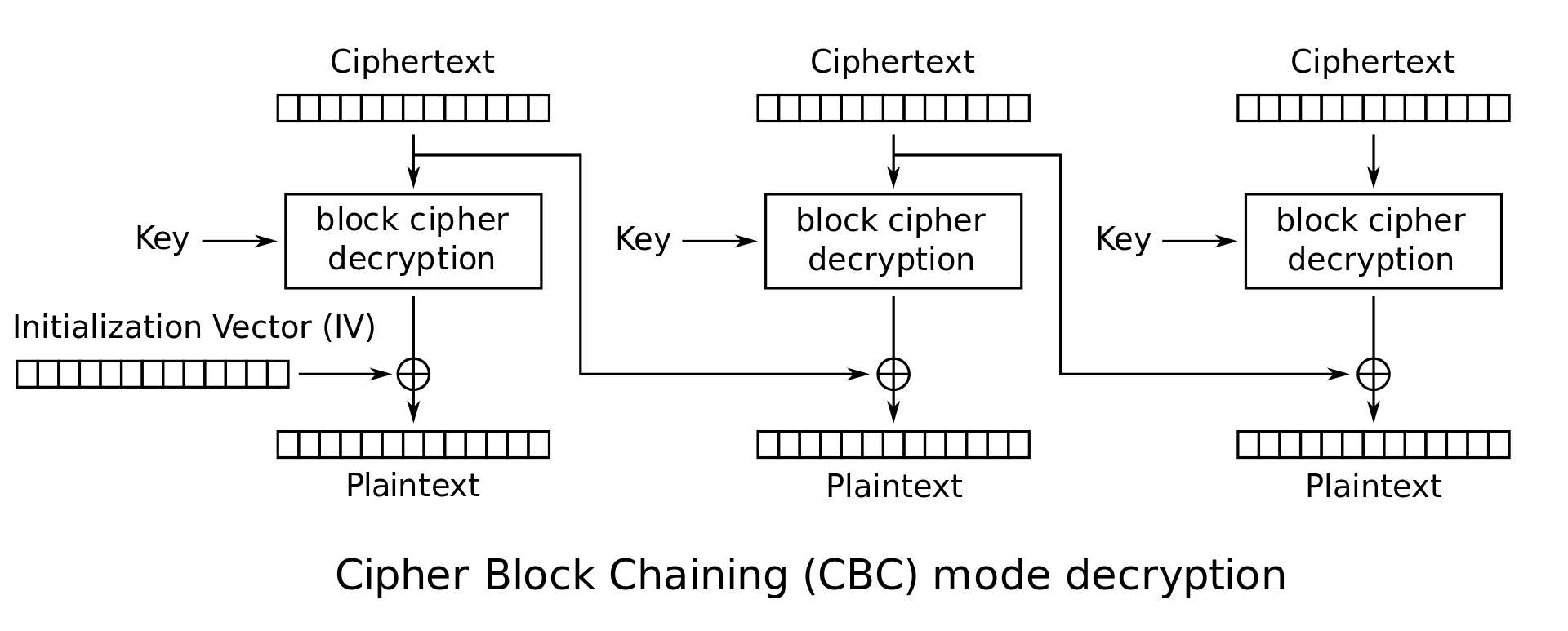
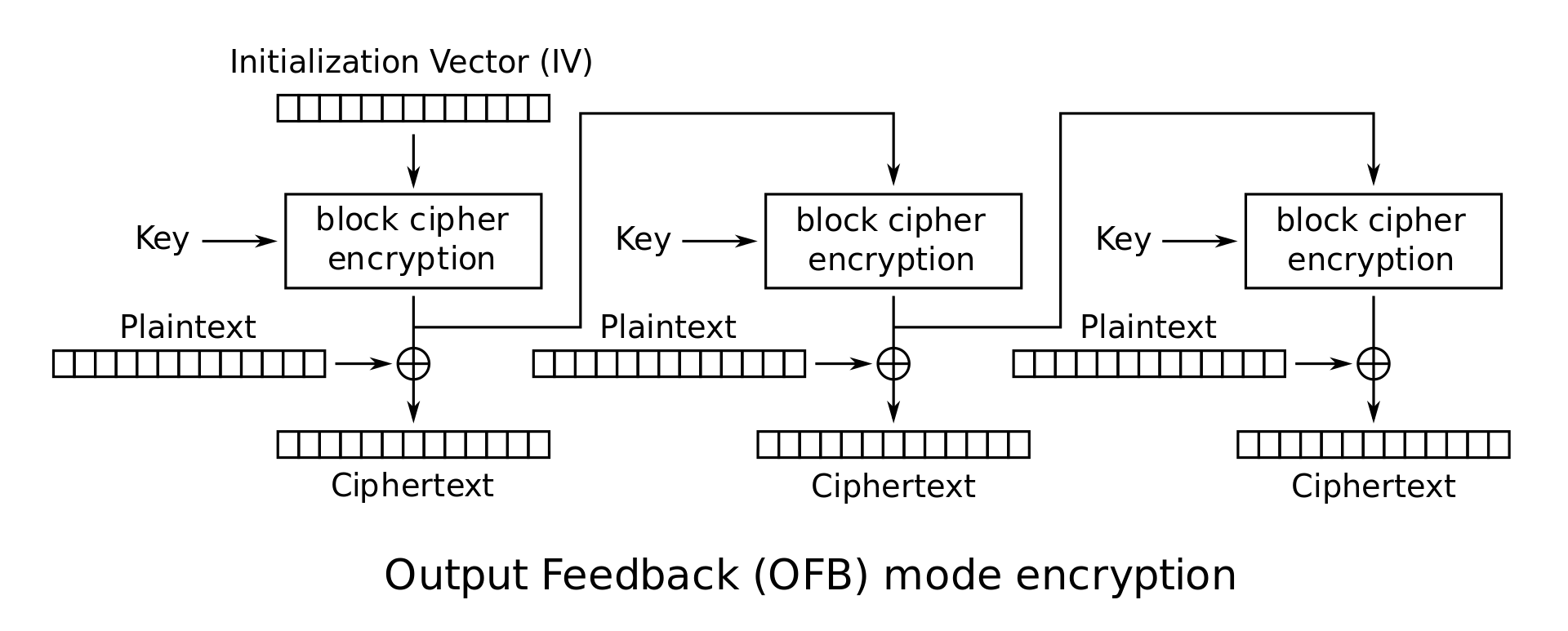
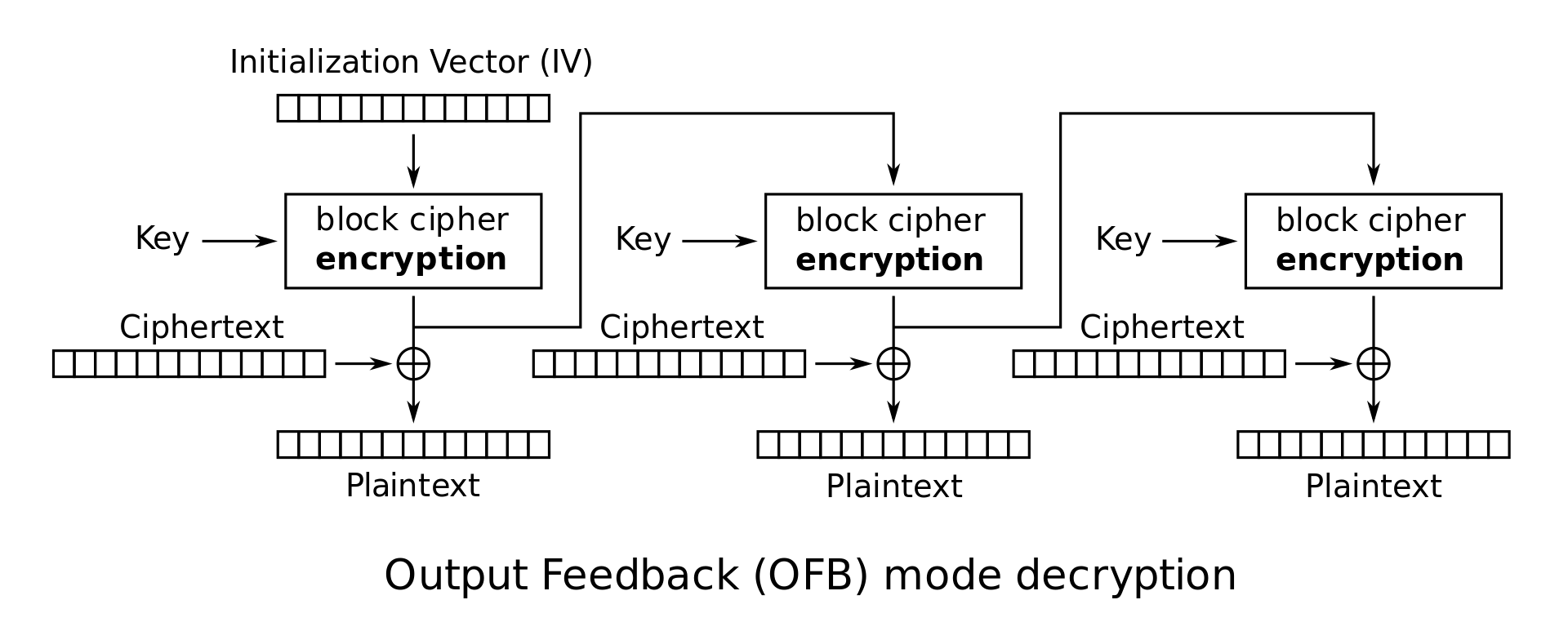
Output feedback (OFB)

• Can prepare encryption and decryption in advance

• Malformed/incorrect blocks affect only the current block

---

Types of Encryption

Symmetric	Asymmetric
Single key	Two linked/related keys
Fast	Slow
Good for large data transfers	Good for small data transfers
Only provides confidentiality	Can provide confidentiality, authentication, and non-repudiation

---

Symmetric Encryption

---

“Perfect” Encryption - One-Time Pad (OTP)

• Major rules of OTP:
  • Key must be the same size as the message
  • Key must be truly random
  • Keys must never be reused

---

One-Time Pad Encryption

---

One-Time Pad Decryption

---

Is One-Time Pad practical to implement?

---

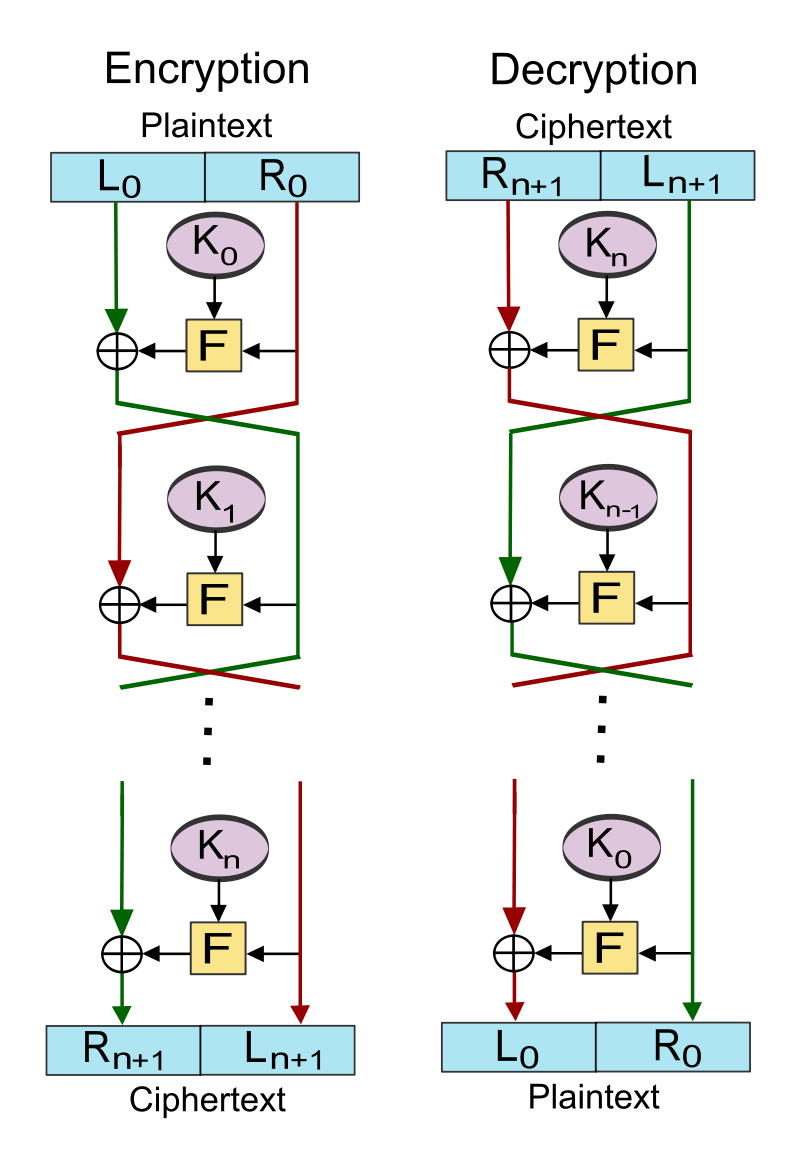
Feistel Cipher

• Created by German physicist Horst Feistel and patented the early 1970’s
• The Feistel Cipher is a design model (template) that is used to create different block ciphers.
  • Blowfish, DES, RC5, Twofish

---

How the Feistel Cipher Works

---

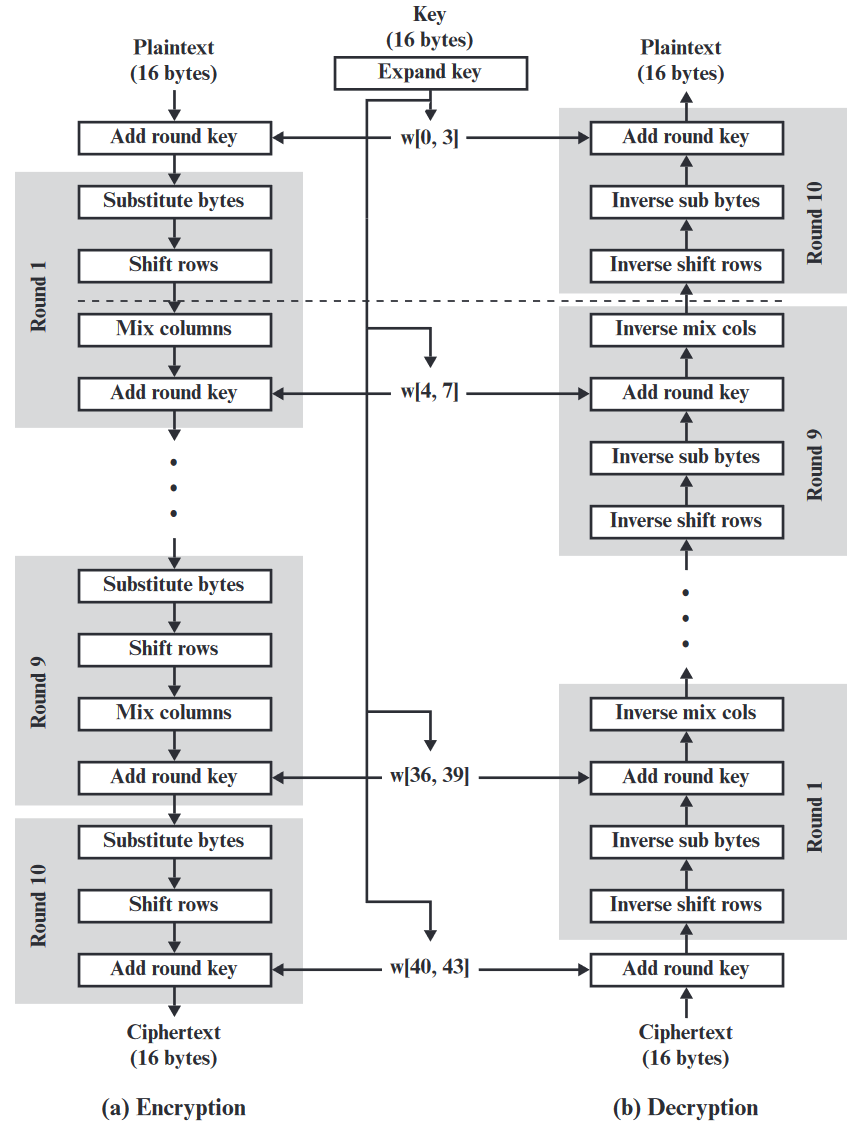
Data Encryption Standard

• A symmetric-key algorithm standardized in 1977
• Incorporates 16 Feistel Cipher rounds
• Has a block size of 64-bits
• Has a key size of 56-bits
  • Purposely neutered by the NSA to make brute-force attacks easier

---

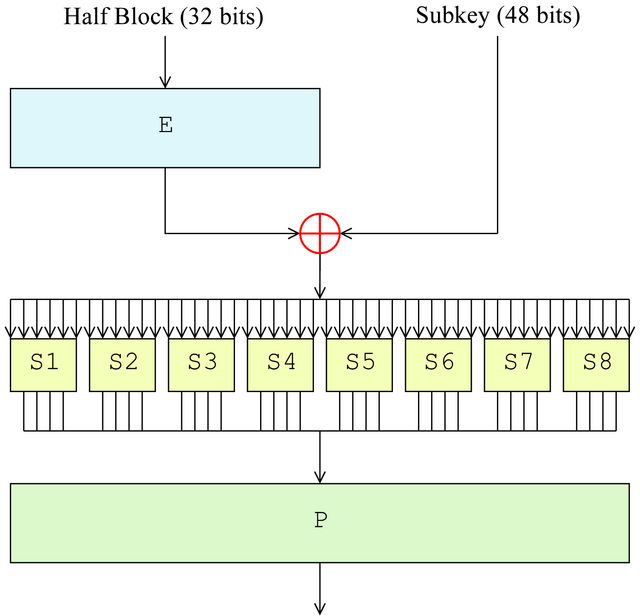
How the Data Encryption Standard Works

• Expansion: Function that takes 32-bit block increased to 48-bits
• Key mixing: XOR operation with the subkey
• Substitution: Lookup table
• Permutation: Bit shuffling

---

Triple DES (3DES)

• Published in 1981
• Incorporates 48 Feistel Cipher rounds
• Has a block size of 64-bits
• Has a key size of 168-bits (three 56-bit keys)
• Officially deprecated by NIST at the end of 2023

---

Advanced Encryption Standard (AES)

• Published in 1998 by Joan Daemen and Vincent Rijmen under the name Rijndael
• Selected by NIST in 2001 to replace DES

	Key length (bits)	Block size (bits)	# of Rounds
AES-128	128	128	10
AES-192	192	128	12
AES-256	256	128	14

---

How AES works (1 of 2)

---

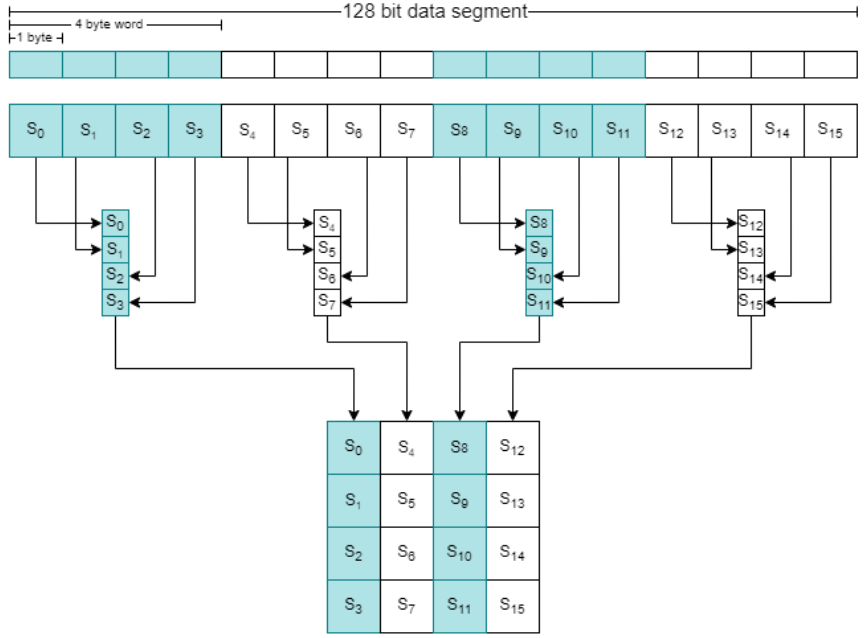
How AES works (2 of 2)

• SubBytes
• ShiftRows
• MixColumns
• AddRoundKey

---

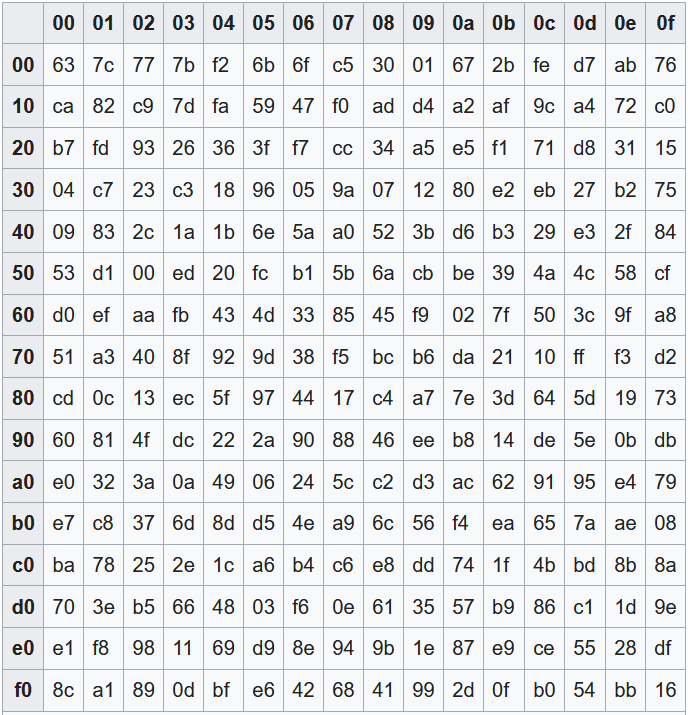
How AES works - SubBytes

• Byte-wise table lookup

---

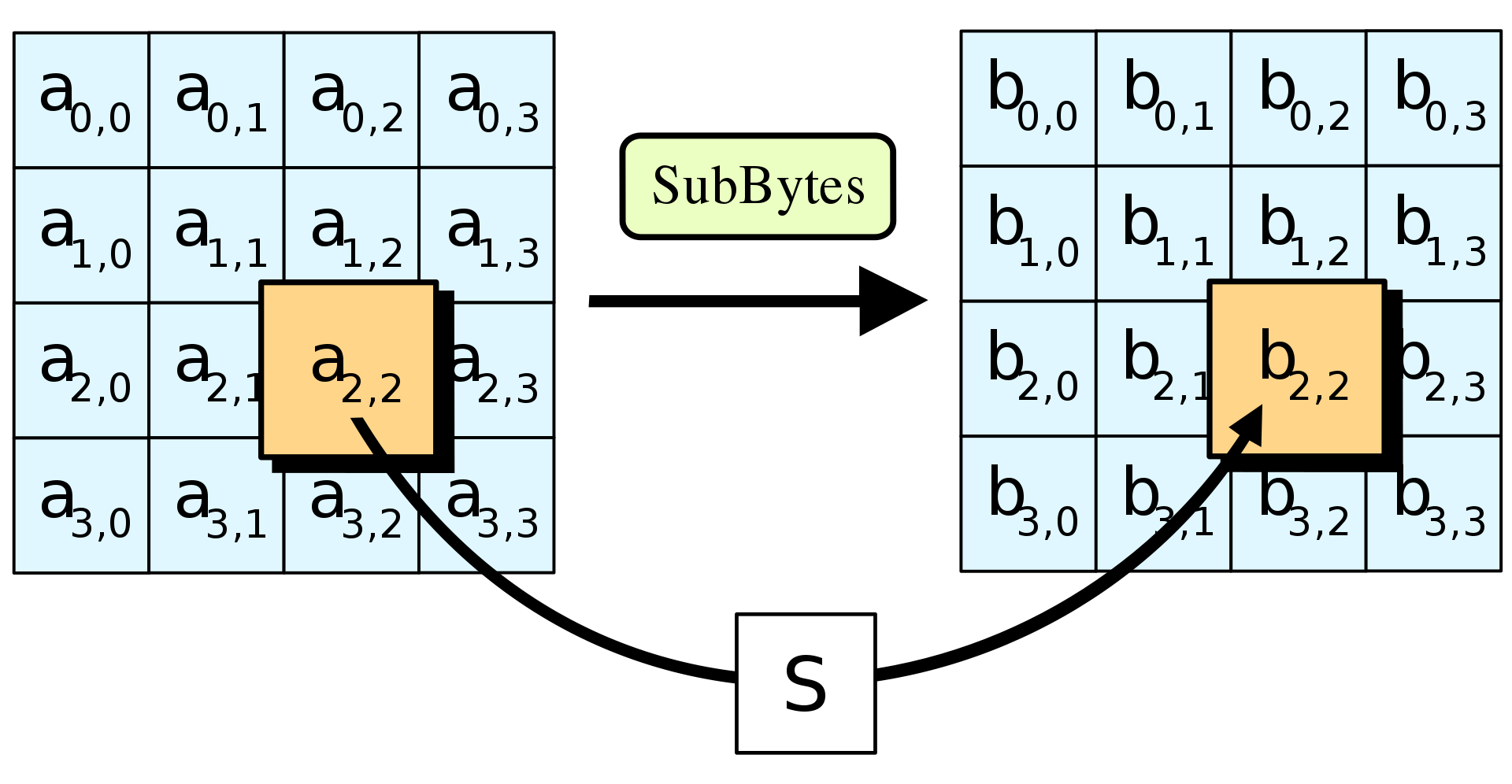
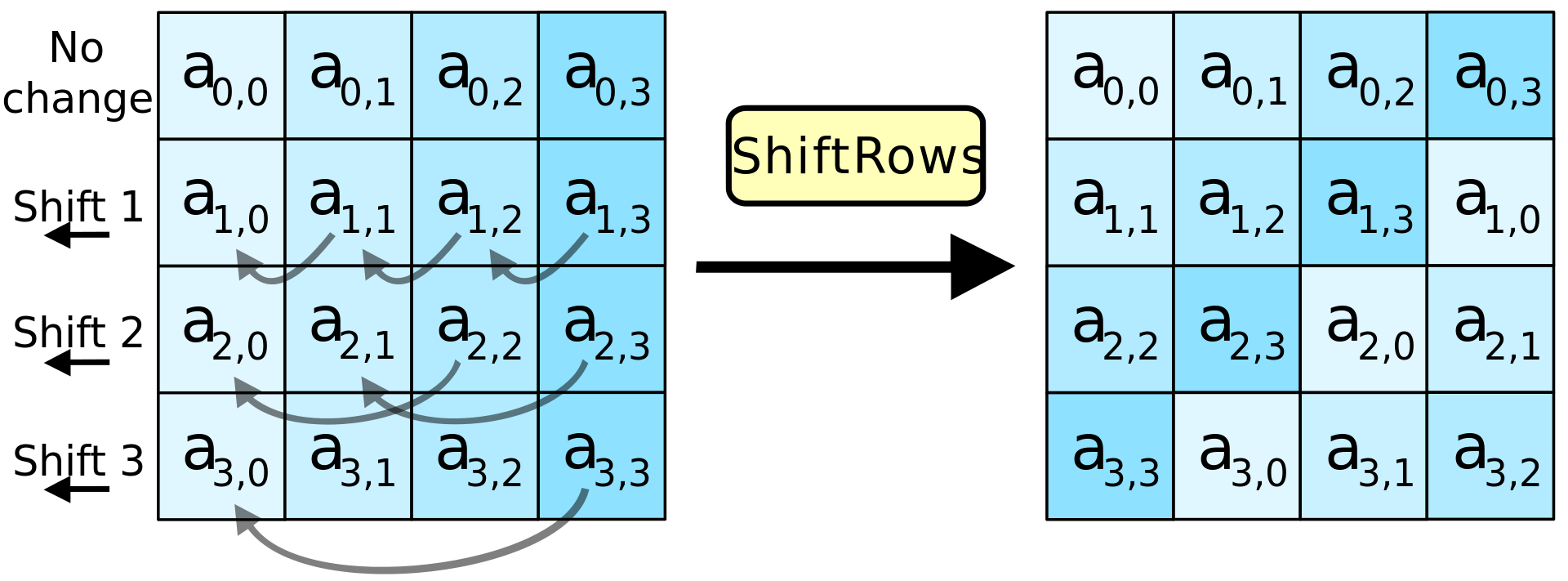
How AES works - ShiftRows

---

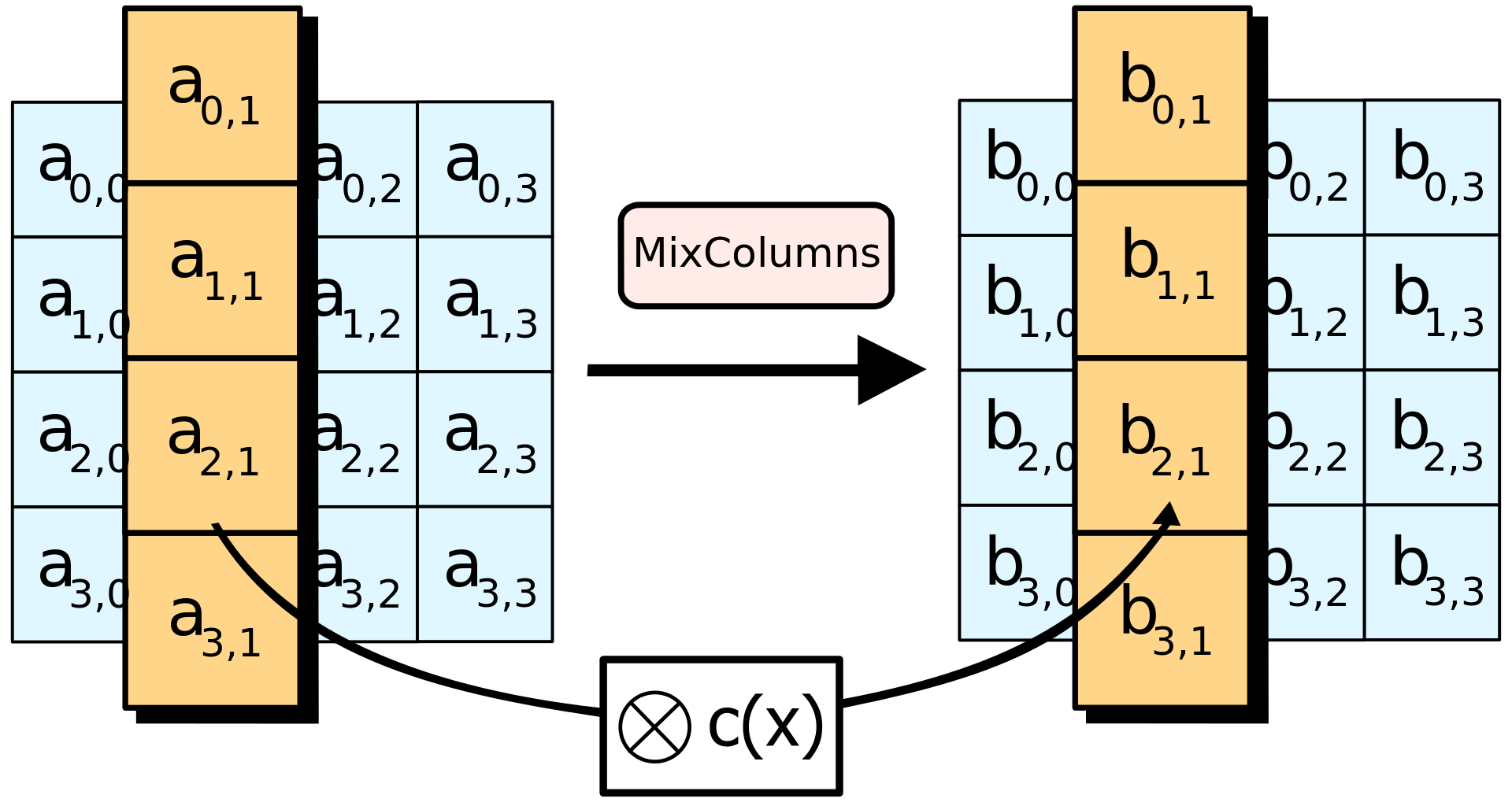
How AES works - MixColumns

• Shuffles bits using special matrix multiplication
  • Uses polynomials, XOR, and modulo

---

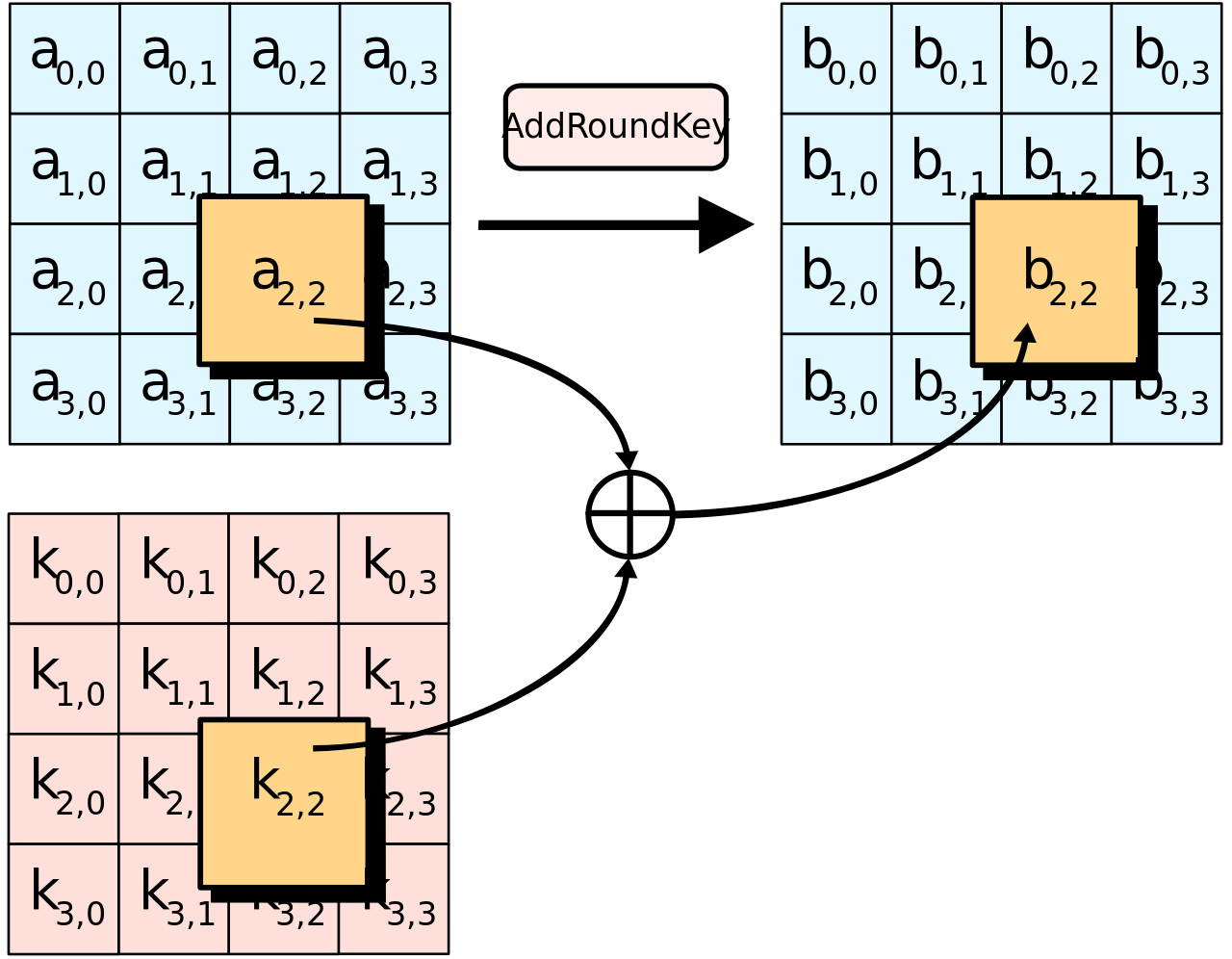
How AES works - AddRoundKey

---

Asymmetric Encryption

---

Diffie Hellman key exchange (DH)

• An asymmetric-key protocol conceived by Ralph Merkle that was published by Whitfield Diffie and Martin Hellman in 1976.

• Previously been discovered by a British intelligence agency in 1969.

---

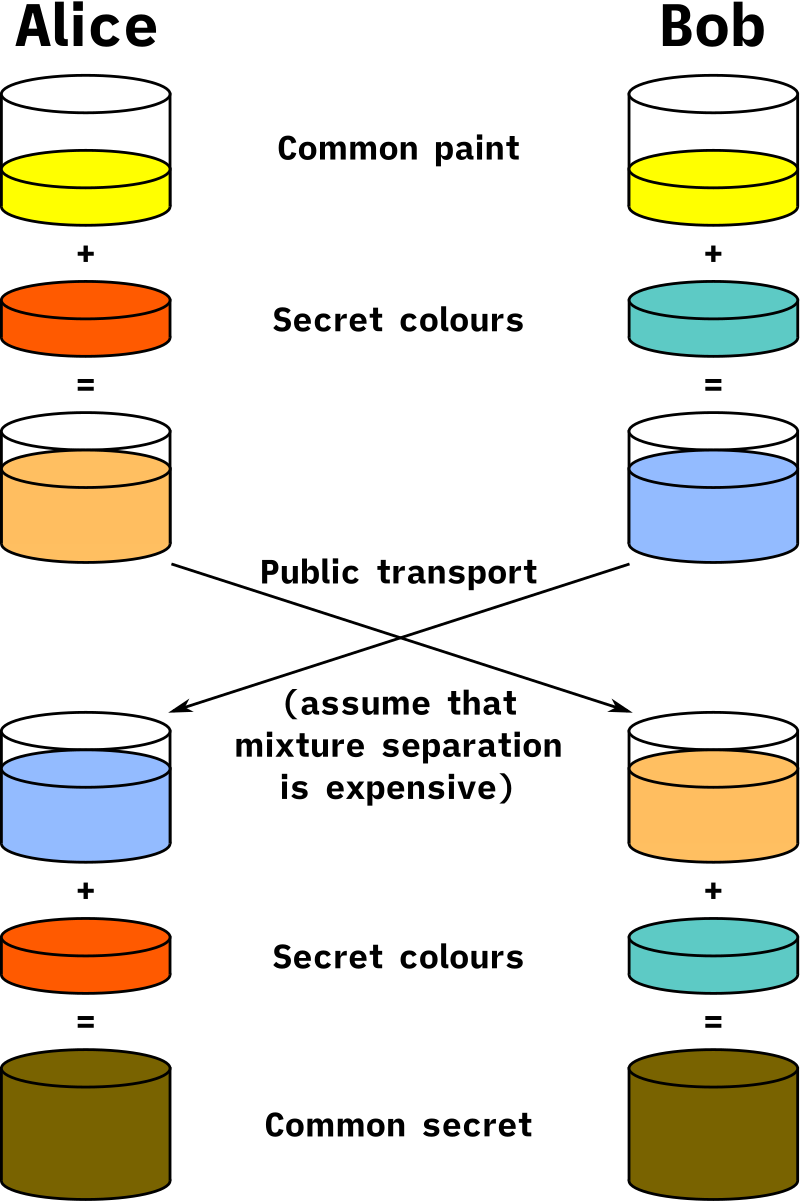
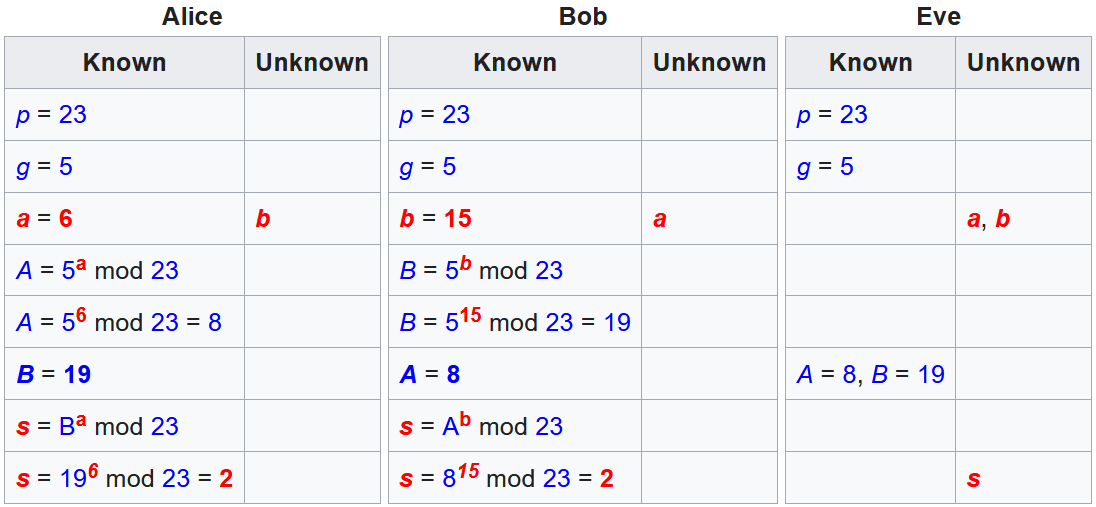
How DH Works (1 of 2)

• Alice and Bob publicly agree to use the modulus p=23 and base g=5

Alice	Bob
α = 4	β = 3
A = gᵃ mod p	B = gᵇ mod p
A = 5⁴ mod 23 = 625 mod 23 = 4	B = 5³ mod 23 = 125 mod 23 = 10
sᵃ = Bᵃ mod p	sᵇ = Aᵇ mod p
sᵃ = 10⁴ mod 23 = 10000 mod 23 = 18	sᵇ = 4³ mod 23 = 64 mod 23 = 18

---

How DH Works (2 of 2)

---

Rivest-Shamir-Adleman (RSA)

• An asymmetric-key algorithm published in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman
• Relies on the difficulty of factoring the product of two large prime numbers
• Common key lengths in RSA
  • 1024, 2048, 3072, 7680, 15360

---

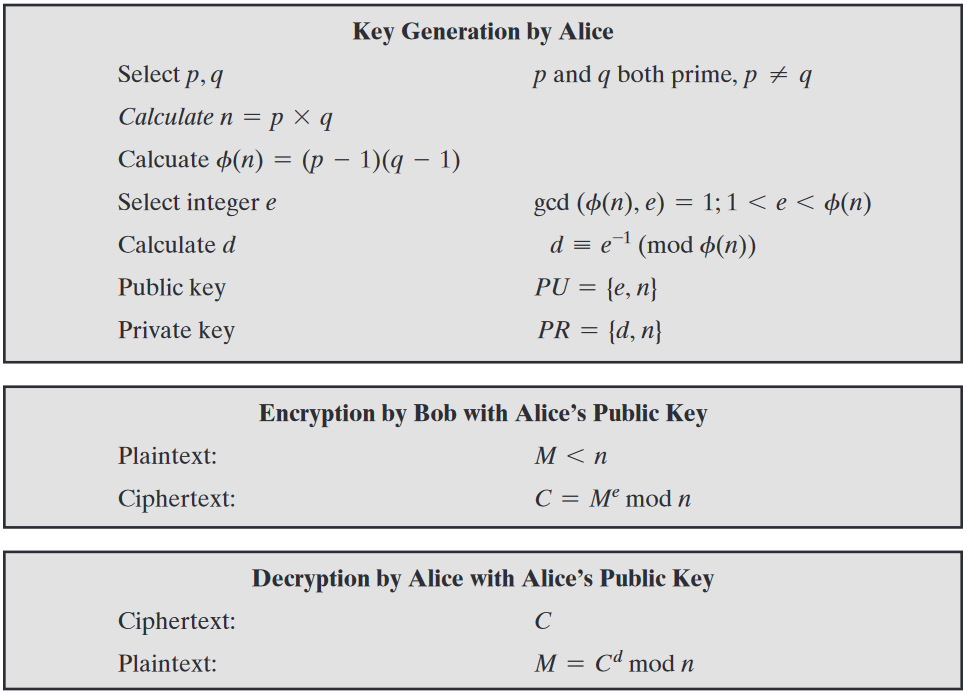
How RSA Works (1 of 2)

• p, q : chosen random prime integers (private)
• n : product of p and q, modulus for the public/private keys (public)
• Φ(n) : (Phi of n) Euler totient
• e : chosen integer that is (public):
  • greater than one and less than the totient
  • co-prime to the totient
  • shares no common factors with the totient
• d : calculated multiplicative inverse of e mod the totient (private)

---

How RSA Works (2 of 2)

• Public key

  • {e, n}

• Private key

  • {d, n}

---

RSA Example (1 of 3)

• p = 5, q = 7

• n = 5 × 7 = 35

• Φ(n) = (5 - 1) × (7 - 1) = 4 × 6 = 24

• e = 1 < 5 < 24

  • can check if co-prime using Euclid’s Algorithm (GCD)

• d = 5⁻¹ mod 24 = 5

  • can solve this using Extended Euclid’s Algorithm (XGCD)

---

RSA Example (2 of 3)

• Public Key: {5, 35}

• plaintext (M): 23

  • ciphertext (C) = Mᵉ mod n

• C = 23⁵ mod 35 = 6436343 mod 35 = 18

---

RSA Example (3 of 3)

• Private Key: {5, 35}

• ciphertext (C): 18

  • cleartext (M) = Cᵈ mod n

• M = 18⁵ mod 35 = 1889568 mod 35 = 23

---

Elliptic-Curve Cryptography (ECC)

• An asymmetric-key cryptography approach independently suggested by Neal Koblitz and Victor S. Miller in 1985.
• Relies on the discrete logarithm problem over the elliptic curve y² = x³ + ax + b
• Elliptic-curve calculations are more computationally demanding allowing keys to be smaller than the equivalent RSA counterparts

---

How ECC Works (1 of 4)

• Publicly agreed on curve (a=2, b=2, q=17):
  • y² = x³ + ax + b
  • y² = x³ + 2x + 2
• Publicly agreed on generator (G)
  • G=(5,1)
• Publicly agreed order of G (n)
  • n = 19

---

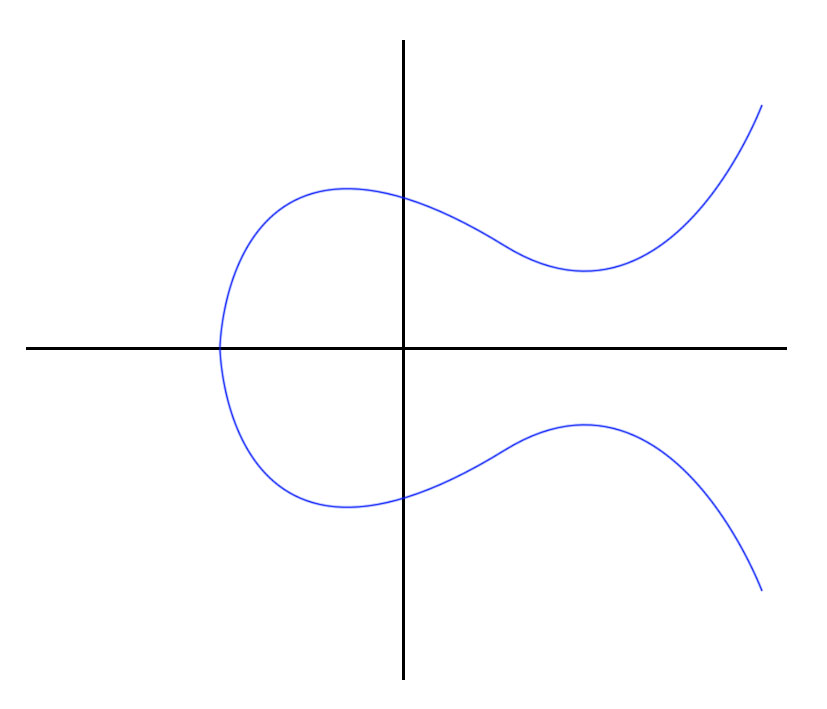
How ECC Works (2 of 4)

• G=(5,1)

Alice	Bob
α = 3	β = 9
Α = 3G	Β = 9G

---

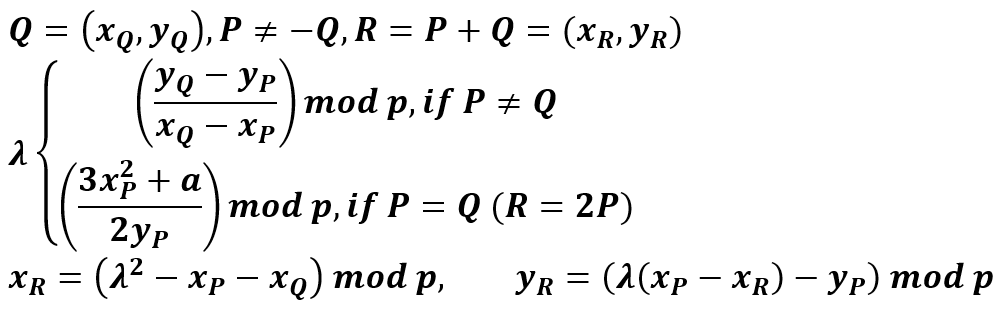
How ECC Works (3 of 4)

• Alice (3G)

  • G + G = 2G
  • 2G + G = 3G (10,6)

• Bob (9G)

  • G + G = 2G
  • 2G + 2G = 4G
  • 4G + 4G = 8G
  • 8G + G = 9G (7,6)

---

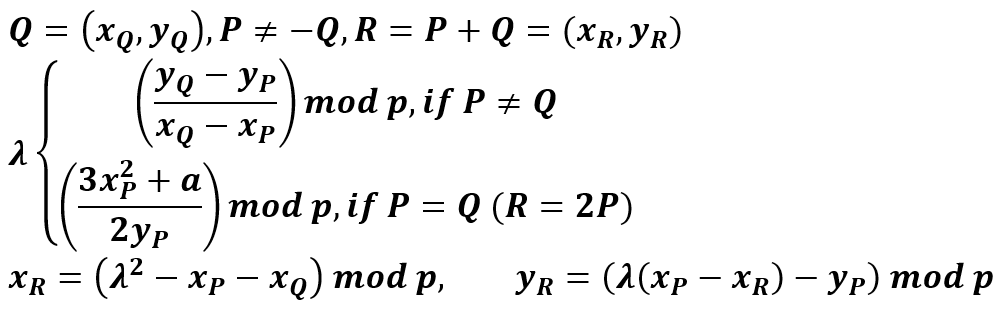
How ECC Works (4 of 4)

Alice	Bob
Α = 3G = (10,6)	Β = 9G = (7,6)
αΒ = 3Β = 3(9G) = 27G = 8G = (13,7)	βΑ = 9Α = 9(3G) = 27G = 8G = (13,7)

---

Comparison of Symmetric and Asymmetric Algorithms

Security Bits	Symmetric Encryption Algorithm	RSA	ECC
80		1024	160
112	3DES	2048	224
128	AES-128	3072	256
192	AES-192	7680	384
256	AES-256	15360	512

---

Symmetric Encryption Quantum Threats

• Grover’s Algorithm

  • A quantum brute-forcing algorithm that is effective against AES

  • Takes AES from O(N) to O(√N)

    • 2¹²⁸ → 2⁶⁴

    • 2¹⁹² → 2⁹⁶

    • 2²⁵⁶ → 2¹²⁸

---

Asymmetric Encryption Quantum Threats

• Shor’s Algorithm

  • A quantum algorithm for finding prime factors of an integer (DH, RSA) and discrete logarithms (ECC)

---

Hashing

---

Password Hashing

• password123

• SHA-256

  • ef92b778bafe771e89245b89ecbc08a44a4e166c06659911881f383d4473e94f

• password123D;%yL9TS:5PalS/d

  • 9C9B913EB1B6254F4737CE947EFD16F16E916F9D6EE5C1102A2002E48D4C88BD

• password123D;%yL9TS:5PalS/d + iterations

  • fc91e3c64406e6afb456303d93ecb7c22b7f7ddb7f89d7e3ca52de8c10c16525

---

Storing Hashed Passwords - LAN Manager

• Morpheus:1010:B902F044A44585DF93E28745B8BF4BA6:D5D630DA69EBD8AB040D77BE7BB046DD:::

• username:user_id:LM_hash:NTLM_hash

• 14 character password

  • Converted to uppercase
  • Unused space filled with null bytes
  • Split in half with parity character added (two 8-byte segments)
  • Both halves are encrypted with DES and concatenated together

---

Storing Hashed Passwords - New Technology LAN Manager

• Morpheus:1002:aad3b435b51404eeaad3b435b51404ee:d5d630da69ebd8ab040d77be7bb046dd:::

• username:user_id:LM_hash:NTLM_hash

• 14 character password

  • RC4 encryption

---

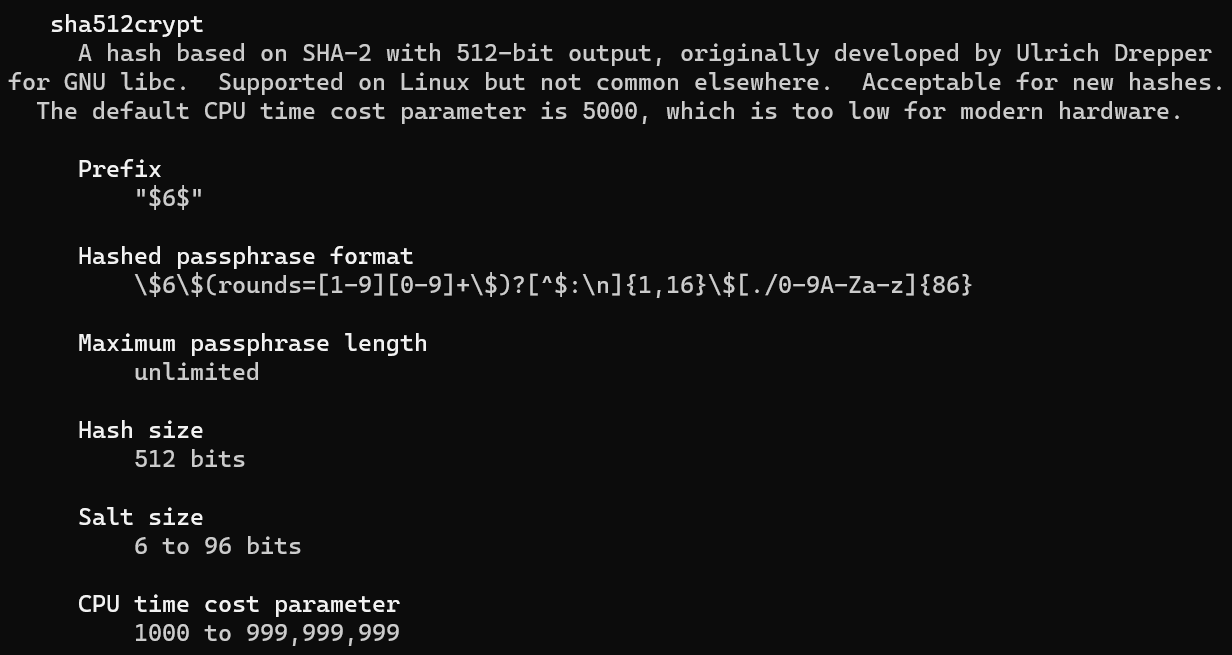
Storing Hashed Passwords - sha512crypt

• Morpheus:$6$ykumbyCz$kb1zUhrB3wROIN1uoI94gfmAMjlTeeVhKkEtEZHYeIFIqD6CBiAQAlFB9uqYHHVO1doCNJbV56tC4gJi/L0ng0:1001:1001::/home/morpheus:/bin/sh

• username:hash_algorithm:user_id:group_id:home_directory:default_shell

---

man 5 crypt - sha512crypt

---

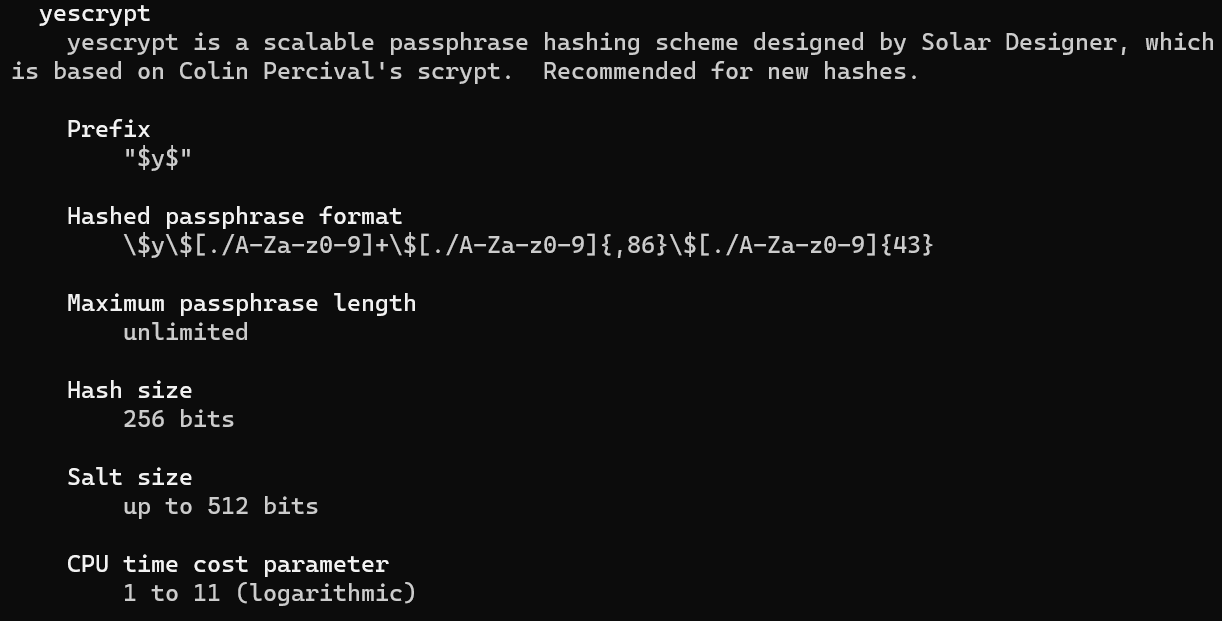
man 5 crypt - yescrypt

---

Password Hashing Explained

• Hashing protects against dictionary attacks

• Salts protect against rainbow tables

  • Precomputed hashes

• Iterations increase the computation time

• Hash + Salt + Iterations:

  • susceptible to dictionary attacks if the algorithm is known